For songwriters who have the fortitude to get past the confusing wheel of music theory death that is the Circle of Fifths, this unique shortcut tool can provide a wide range of benefits. In fact, it's not very difficult to memorize, and once you know it like the bank of your hand, you'll be able to easily navigate through chord progressions , key signatures, and more!
Now, you may remember the Circle of Fifths from your high school music class, or you may be new to the concept altogether. Whatever the case, we're going to take you through a step-by-step guide, so you never get confused again!
Why Learning the Circle of Fifths Is Important
To be completely honest with you, you may not find yourself using the Circle of Fifths ever.
Does that make you an amateur musician or songwriter?
No way! However, we find that it can be a beneficial tool for understanding how key signatures are derived and how chord progressions work. The visual aspect of the Circle of Fifths is what makes it so helpful, as you can keep the visual in your brain every time you're feeling musically disorganized.
It's important to note that just about every piece of western music follows some type of pattern . Of course, they do the same things in Eastern music as well! These patterns, called scales or modes, take us on journeys through musical pieces and bring us back home safely. Different patterns make us feel certain ways, and when you learn how to manipulate the listener's emotions using these patterns, you've reached true musical mastery.
So, the question then becomes,
How in the world does this thing work?
But First, Some Basic Music Theory
If you already have a basic understanding of music theory, you can head down to the next section. However, if you're new or feel like you could use a good fundamental refresher, then keep reading.
Key Signatures
Key signatures are musical groupings of seven notes that compositions are made out of. When playing a song in a given key, you can use the included notes from progressions and melodies that sound pleasing and musical.
In written music, key signatures are represented as sets of accidents (sharps or flats) that define the musical pitches in the key. There are 12 keys (24 if you're counting major AND minor), which are made from the 12 keys on the piano.

Sharps and Flats
Sharps and flats, otherwise known as accidentals, are semi-tones or half-steps between the seven notes of the musical alphabet: C-D-E-F-G-A-B.
Ac accidental is placed after one of these letters to tell you whether the note is a half-step up or down from the letter note.
If we added a sharp symbol (#) to the note C to make C#, you would play it one half-step up from C.
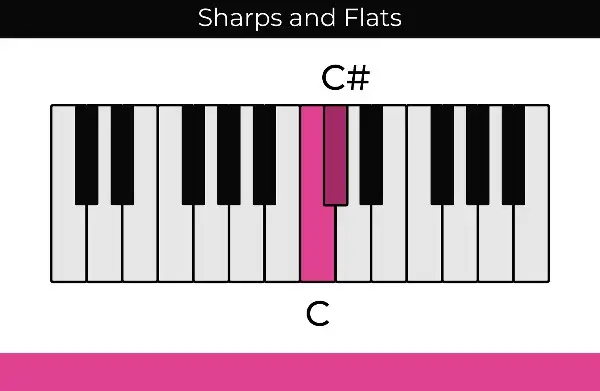
On the other hand, if we added a flat symbol (b) onto the note G to make Gb, you would play it one half-step lower than G.
Understanding how sharps and flats work is critical in understanding how the circle of fifths works, as accidentals tell us what keys we're in, and the circle of fifths is made of key signatures.
The Foundation of The Circle of Fifths
The very first pattern you need to be aware of on the Circle of Fifths is the pattern of key signatures .
A key is a collection of seven notes, of which together we refer to as a scale . We build scales using specific relationships between the notes in a scale. For example, the relationships between the notes of a scale in a major scale or minor scale are different.
To start, let's look at the notes of a C Major Scale:
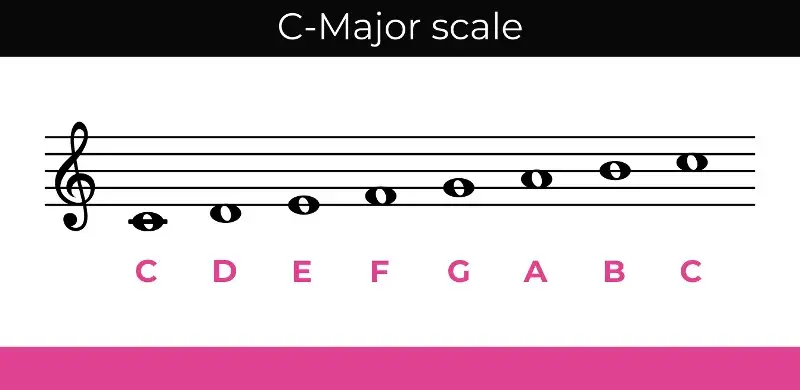
At the beginning of the C Major Scale is the note "C," otherwise known as the tonic . From C, you move up one note at a time through the scale until you reach the following note C , which is an octave . You'll notice that these are the same notes when played together, though one is higher than the other.
If you were to play these notes out on a keyboard, it would be 12 half-steps to reach the octave, moving one note at a time. Now the reason this is important is that it gives us a frame of reference when we think about fifths.
The perfect fifth in the C Major Scale is G , as G is the fifth scale degree in the scale. However, it's important to note that a fifth is actually seven half-steps up from the root or tonic C , not five. The same thing applies to both major and minor keys.
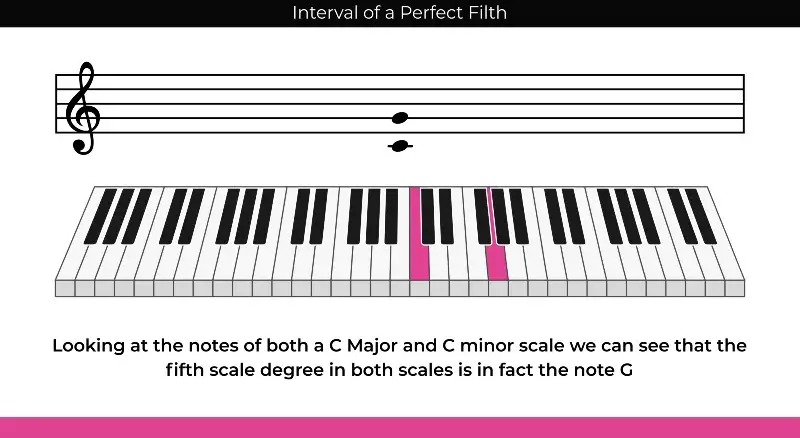
So, if we look at the Circle of Fifths illustration below, we can see that the next letter over (moving clockwise) from C is G , as G is a perfect fifth above C. If we move one more letter over from G, we get to B, as B is a perfect fifth interval from G, and so on.
On the other hand, if we move counter-clockwise, we move in fourths instead of fifths. So, for example, if we start at C and move one letter counter-clockwise, we get to the note F , which is a perfect fourth (five half-steps) from C. Sometimes, people will use the term "Circle of Fourths" when referring to this same circle counter-clockwise, though, for the purpose of this article, we'll focus on the clockwise portion.
Now, if you were wondering, the reason we refer to each successive fifth as a "perfect fifth" it's because the fifth remains the same, regardless of if the key is major or minor. A third, sixth, and seventh will change depending on whether you're in a major or minor key.
The idea here is that it's important to understand what a fifth sounds and feels like to know why we've put them on this musical pedestal.
The Circle of Fifths In Accidentals

There are many musicians who find it easier to think of the circle of fifths by the number of accidentals found in the different key signatures. To give you examples of how this works, we'll start with C.
Basic music theory tells you that the key of C major does not have any accidentals (sharps or flats). So, if you start with the key of C major on the circle of fifths and move clockwise to the next step, you'll land on G Major, which has a single accidental — F#.
Continue going around the circle clockwise and you'll see that each step adds one more sharp.
While many piano players must learn the order of sharps when learning to play the piano, it can be difficult for some people to remember. For those people, we have a helpful mnemonic device:
- F ather
- C ars
- G o
- D angerously
- A round
- E very
- B end
You will continue bouncing around the circle of fifths in a clockwise fashion, adding one sharp with every step until you get to C#, which has seven sharps !
Now, of course, you might be asking, what about moving counter-clockwise in the circle from C major?
Starting with C and moving counter-clockwise, you move down a fifth with each successive step while adding a flat.
A helpful mnemonic device to remember these flats is:
- B attle
- E nds
- A nd
- D own
- G oes
- C harles
- F ather
The first step counter-clockwise is F , which contains one flat, and the next step is Bb , which contains two flats. Keep moving until you get to Cb Major , where you'll find seven flats!
The Circle of Fifths - Minor Keys
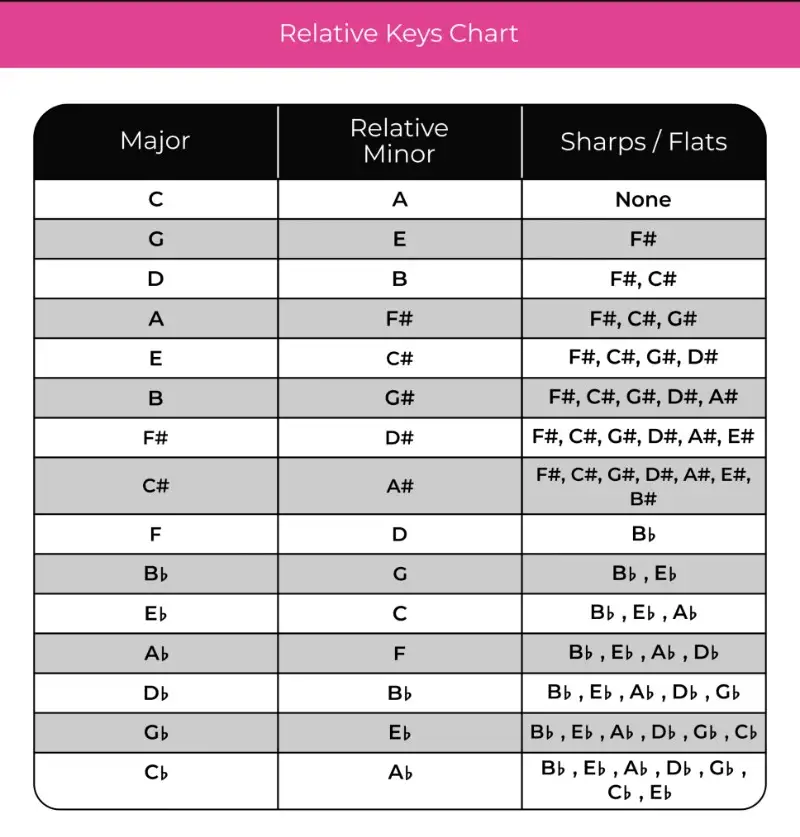
By this point, you should have a decent understanding of how the major keys are arranged on the circle of fifths. Now, let's look at the minor keys.
The beauty of major and minor keys is that they share key signatures. If you start in the correct spot, you can add sharps and flats the same way you did with major keys.
Every major key has a relative minor key that begins on the major scale's sixth scale degree. So, for example, if you're in the key of C Major and you count up six scale degrees, you'll get to A, which is the relative minor key.
This means that A minor shares the exact same key signature as C major without any flats or sharps. The exact same thing goes for every major key in the circle. For example, if you start at G major and count six scale degrees up, you get to E, which is the relative minor of G major.
Practical Applications for the Circle of Fifths
You can think of perfect fifths as the building blocks of western music theory. For many centuries, composers and songwriters used the circle of fifths to build chord progressions, harmonize melodies, and change keys during a piece of music. The beauty of the Circle of Fifths is that it provides a road map for diatonic chords and functionality.
You can look at just about any great piece of Western music and fit it into the Circle of Fifths to make sense of it. From Beethoven to Brahms to the Beatles to Britney Spears, all great musicians have used the Circle of Fifths in some way or another, whether they recognized it or not.
Let's dive in and check out some of the more practical applications of this music theory tool.
Finding The Right Notes In a Key Signature
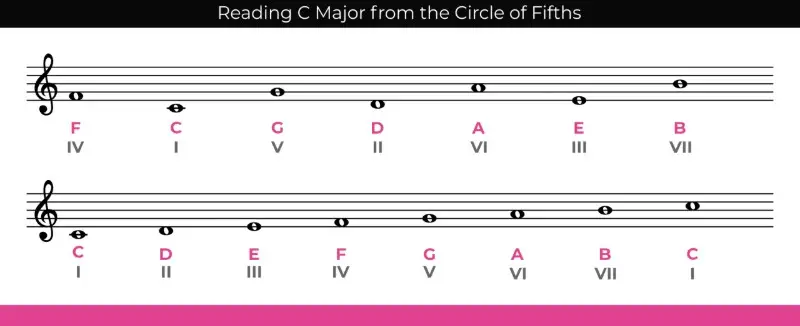
While it's a good idea to know the notes of your key signature, you find the notes found in any of the major scales by starting at the immediate counter-clockwise note in a major key and counting the seven notes clockwise .
Once you have the seven notes, you can rearrange them into the correct scale order to get your diatonic scale!
So, for example, let's say you want to figure out the chords in C major. You could start one note counter-clockwise, which is F , and count the next six notes in the scale — C-G-D-A-E-B.
Finding Relative Major and Minor Keys
As you know now, all major keys have relative minor keys with the same number of accidentals. The only thing you have to do to find a relative minor key is move three steps clockwise . IF you're looking for a relative major key, you can move three steps counter-clockwise .
PRO TIP: One of the coolest ways to use relative minor keys is during the bridge of a song. Because a minor key uses all of the same notes as its relative major key counterpart, you can create a familiar-sounding bridge that provides a uniquely opposite mood and feel.
Building Chord Progressions
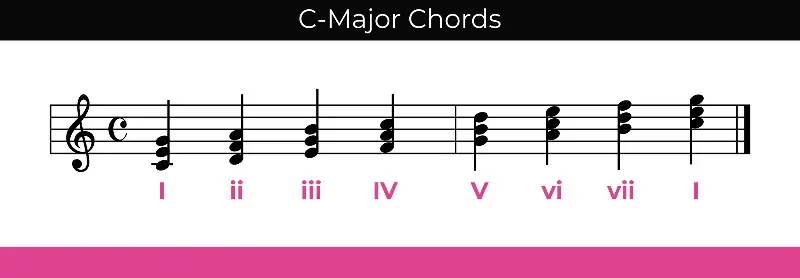
Take a look at popular music from the past 100 years and you'll see that people often recycle the same chord progressions over and over again. Arguably, the most popular chord progression in western music is the I-IV-V-I .
Now, if you're unaware of Roman numerals in music theory, they are used to denote the different scale degrees. In the case above, the I-IV-V-I notation represents chords 1-4-5-1 in the major scale.
In a major scale, the I-IV-V-I chord progression is made up of all major chords, including the tonic, the fourth, and the fifth. If you start in the key of C major and move through these chords one at a time, we guarantee you'll recognize the tonality and cadence.
So, if you start with the key of C major and look at your circle of fifths, you'll immediately see the fourth and fifth to the right and left of the note C, allowing you to create the most basic chord progression in a matter of seconds!
Now, if you take a single step past the fourth and fifth on each side, you'll get to the second and seventh, which are great for expanding chord progressions and making them more unique. Even sticking to these five chords and using these groupings of notes played together can provide you with a consonant chord progression.
Note that when it comes to Roman numerals, major chords are denoted with capital letters while minor chords are denoted with lowercase or non-capital letters.
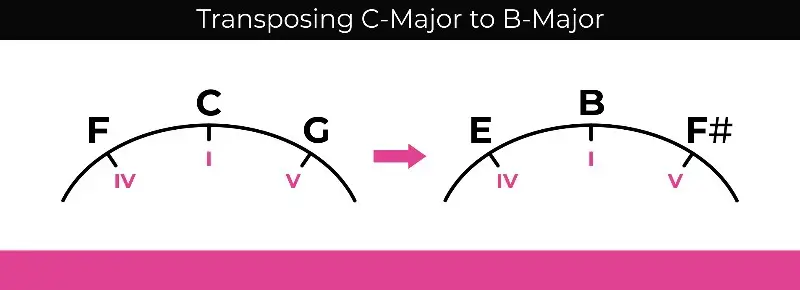
Transposing a Song
Transposition is very similar to modulation, which is why many new musicians often confuse the two terms and use them interchangeably when talking about musical composition. However, when transposing a song, the goal is to use the exact same chord progression in a different key.
Composers will often transpose songs for vocalists if they're not comfortable with the range. The beauty of using the circle of fifths to transpose a song is that all you have to do is find the tonic you want to use and find the same chords using the same shape relationship.
So, for example, let's say that you're using the basic I-IV-V-I progression, but you want to transpose the song a step down from C major to B major. Well, you already know that your tonic is I (your C major chord), a step clockwise is V (your G major chord), and a step counter-clockwise is IV (your F major chord).
To transpose the song from C major to B major, you can simply rotate the entire circle and use the same shapes.
Borrowing Non-Diatonic Keys
At some point or another, you'll want to branch out of only using diatonic chords (chords found naturally within a key signature).
In fact, some of the best progressions out there use chords borrowed from other keys. Many people refer to chords outside of key signatures as "borrowed chords." You can use them to add a unique tonal element to your song.
A good place to start with borrowed chords is using secondary dominants. A secondary dominant is the fifth of the fifth of a key signature — V/V.
So, if you're in the key of C major, the fifth chord is a G major chord. The dominant or fifth chord in G major is B major, which you could use as a borrowed chord outside of the C major signature to create interest. You can do the same thing with the subdominant of the fifth as well — IV/V.
There are many ways to use borrowed chords, and the circle of fifths can simply help you find the ones that make the most sense to use.
Modulation
While many songs will use the same key signature throughout, there are many that make use of modulation — the act of changing key signatures during a song.
Changing the key signature during your song can give your listeners a fresh perspective after long, repeated sections. While it's possible to shift to a new key signature directly, smoothly shifting to a new key signature using related keys is far more interesting.
With the circle of fifths, you can see which key signatures gel the most with the current key signature you're working in. For example, you already know that G major only has one more sharp than C major. So, you can smoothly transition from C major to G major without it feeling jarring for anyone listening.
There are many keys that share a few of the same chords, often referred to as "pivot chords." When trying to modulate from one key to the next, it's a good idea to use these pivot chords to offer a smoother transition.
For example, if you wanted to use the key of C major, you could use A minor as a pivot chord, as both C major and G major have the chord A minor.
Final Thoughts - Learning to Love the Circle of Fifths
There's a reason why the beginnings of most music theory courses focus on the circle of fifths. It's everywhere in music!
We hope that you can now see it as a helpful foundational tool rather than a mundane technical concept, as it can help you navigate the world of music theory with ease!