אם לא היו לנו מרווחים במוזיקה, לא היו לנו קנה מידה, מנגינות או התקדמות אקורדים. במובן מסוים, מרווחים הם הבסיס למוזיקה עצמה.

עם זאת, עבור יותר מדי מוזיקאים חדשים, אפילו תורת המוזיקה הבסיסית יכולה להיראות מאיימת.

במדריך הקטן הזה, אנו הולכים ללמד אותך את כל מה שאתה צריך לדעת על מרווחים במוזיקה וכיצד תוכל לסווג אותם כדי להפוך את יצירת המוזיקה למהנה יותר!

מהו מרווח?

מרווח הוא המרחק בגובה הצליל בין שני תווים.

ככל שהמרווח קטן יותר, כך יש פחות הפרש גובה בין שני התווים הללו. מצד שני, ככל שהמרווח גדול יותר, כך ההבדל בין שני התווים גדול יותר.

אנו יכולים לסווג מרווחים בדרכים רבות, אם כי ישנם שלושה אלמנטים עיקריים שאנו אוהבים להסתכל עליהם בעת תיאור מרווח:

• מרחק המגרש של המרווח
• איכות המרווח
• בין אם המרווח הוא הרמוני או מלודי

לפני שנכנס לעומק של כל זה, בואו נסתכל על שני סוגי המרווחים הבסיסיים ביותר שיש - גוונים וחצי גוונים.

צלילים וחצי גוונים

צלילים וחצי גוונים (שלבים שלמים וחצי צעדים, בהתאמה) הם מרווחי היסוד.

כדי ליצור סולמות ואקורדים שונים, נשתמש במגוון שילובי טון וחצי טון.

חצי גוונים הם המ רווח הקטן ביותר של החבורה. לעתים קרובות אנשים מתייחסים לחצי טון כאל חצי צעד.

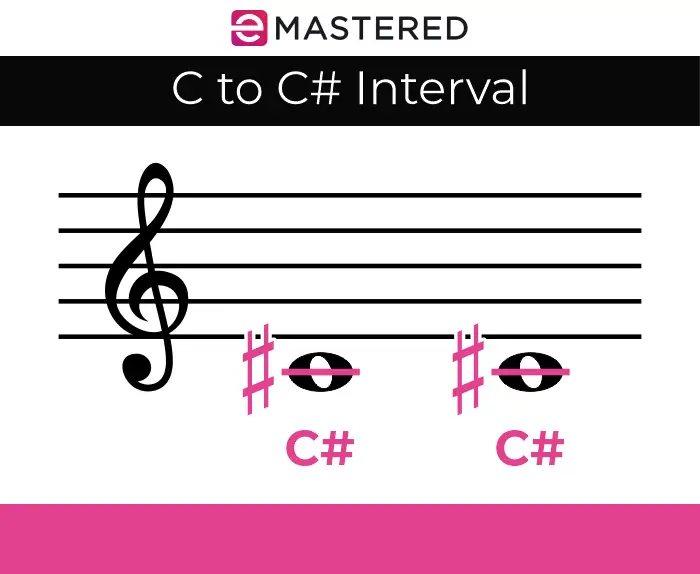
כך, למשל, אם אתה נמצא על הפתק C במקלדת שלך ועובר לתו C #, זהו חצי צעד.

גוונים כפולים מגודלם של חצי גוונים, ורבים מתייחסים אליהם כאל שלבים שלמים. אתה יכול לחשוב על קפיצת מרווח זו כשני חצי גוונים.

כך, למשל, אם אתה נמצא על הפתק C במקלדת שלך ואתה עובר לתו D, אתה מזיז צעד שלם.

שמות מרווחים

כעת, לאחר שיש לך הבנה הגונה של שני המרווחים הבסיסיים ביותר, בואו נסתכל על כמה מרווחים גדולים יותר וכיצד נוכל להגדיר אותם.

כדי להגדיר מרווח, אנו משתמשים במספרים. המספרים מבוססים על מספר שמות האותיות המוזיקליות בין שני התווים.

נניח שיש לנו את התווים C ו- D ממש אחד ליד השני, ואנחנו מנסים להבין את שם המרווח, אנחנו יודעים שהעובדה ש- C ו- D הם שני שמות אותיות זה מזה הופכת את זה לש נייה.

עם זאת, אם ניקח את הפתק D ונעביר אותו ל- E, המ רווח הופך לשליש מכיוון ש- C ו- E הם שלושה תווי אותיות זה מזה.

אם נעביר את ה- E עד F, המרווח הופך לרביעי.

אם נעביר את ה- F עד G, המרווח הופך לחמישית.

אם נעביר את ה- G עד A, המרווח הופך לשישי.

אם נעביר את ה - A עד B, המרווח הופך לשביעי.

אם נעביר את ה- B עד C, המרווח הופך לשמיני או לאוקטבה

חשוב גם לציין שיש לנו שם מרווח כאשר אנו מסתכלים על שני תווים זהים. מרווח זה נקרא יוני סון.

לדוגמה, שני מכשירים בניקוד עשויים לנגן את אותו תו בו זמנית.

איכות מרווח

איכות מרווח היא האלמנט הבא שיש לקבוע.

כשמתייחסים למרווחים, אנחנו לא מתייחסים רק למספרים שלהם. במקום זאת, אנו מבחינים ביניהם על סמך איכותם.

אם נסתכל על התמונה למטה, נוכל לראות ששני המרווחים בצוות הם שלישים.

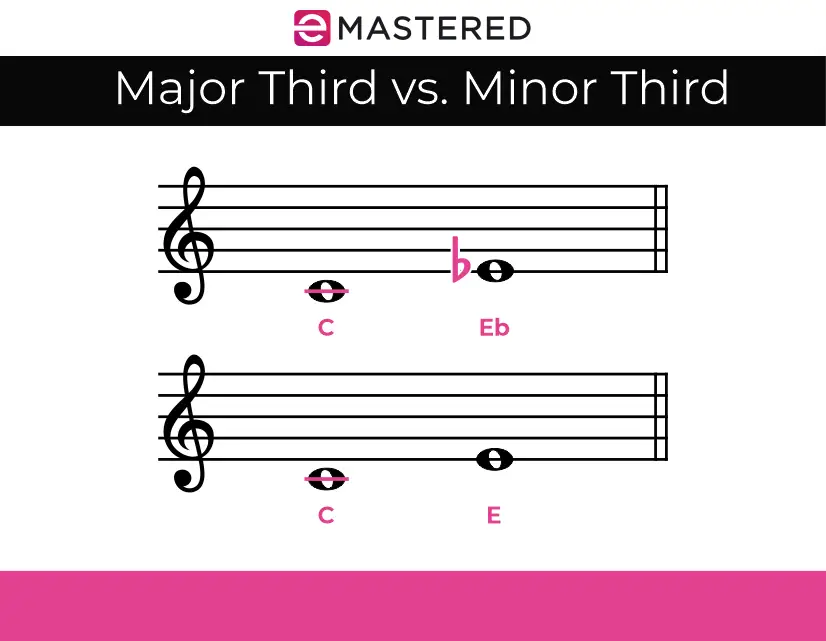
במרווח הראשון יש שלוש הערות אותיות העוברים מ- C ל- E b (C-D-Eb).

הפנימי השני כולל גם שלוש הערות אותיות הנעות מ- C ל - E (C-D-E).

כדי להבדיל בין שני המרווחים הללו זה מזה, עלינו להבין איזו איכות מפרידה ביניהם.

ישנם כמה סוגים של תכונות בעולם המרווחים, כולל:

• מרווחים מושלמים
• מרווחים עיקריים
• מרווחים קלים
• מרווחים מוגברים
• מרווחים מופחתים

לפני שנכנס לאופן הפעולה של סוגי המרווחים השונים הללו, בואו נסתכל על הס ולם העיקרי.

כל תו בסולם הראשי, החל מתו הטוניק או השורש, מהווה מרווח מרכזי או מרווח מושלם:

להלן המרווחים בסולם הגדול C:

מרווחים מושלמים

אנו מתייחסים לשלושה סוגים של מרווחים כמרוו חים מושל מים, כולל:

• רביעי מושלם
• החמישי המושלם
• השמינית המושלמת (אוקטבה)

אלה מרווחים המתרחשים באופן טבעי בקנה מידה העיקרי. אנו מתייחסים אליהם כאל מרווחים "מושלמים" בגלל האופן שבו הם נשמעים יחד ויחסי התדרים שהם מרכיבים.

יש רבעים וחמישיות שאינם מרווחים מושל מים, שאליהם ניכנס בהמשך.

עם זאת, כדי לתת לך ויזואלי טוב יותר, הנה כל המרווחים המושלמים בתורת המוזיקה:

מרווחים עיקריים

אנו מתייחסים לארבעה סוגים של מרווחים כמרו וחים עיק ריים, כולל:

• מייג'ור שני
• מייג'ור שלישי
• מייג'ור השישי
• מייג'ור שביעי

אם אתה מסתכל על הסולם העיקרי, והתו העליון אינו מרווח מושלם, אז אתה יכול לקבוע שזה מרווח מרכזי.

בכל פעם שאתה מחפש את מספר המרווח, אתה יכול להתחיל עם האות הנמוכה ביותר במרווח ולתייג אותו כאחד (שורש או טוניק). לאחר מכן, אתה יכול לספור כמה אותיות דרושות כדי להגיע לתו הגבוה יותר.

להלן המרווחים העיקריים בסולם C major:

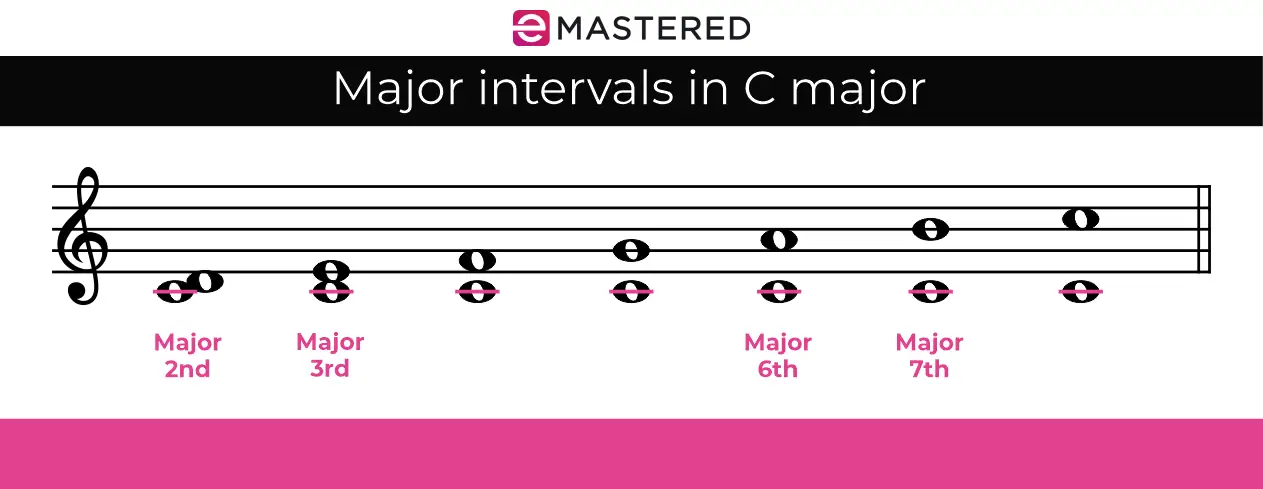
כמובן, אותו דבר חל על כל קנה מידה גדול, לא רק C מז'ור.

אם אתה מתחיל על הטוניק ועובר לפתק שמעליו, הוא יהיה גדול או מושלם.

מרווחים קלים

כאן הדברים מתחילים להיות קצת מסובכים. אם אנו מורידים את התווים העליונים של אחד מהמרווחים העיקריים שלנו בחצי צעד או חצי טון, הם הופכים למרווחים קלים.

נניח שיש לנו את המרווח C עד E, כפי שדיברנו לעיל. מרווח זה הוא שליש מרכזי. עם זאת, אם אנו מורידים את ה- E עם דירה, הוא הופך ל- Eb. המרווח, שהוא כיום C עד E b, הופך לשליש מינורי.

מכיוון שיש לנו רק ארבעה מרווחים עיקריים אפשריים בקנה מידה העיקרי, יש לנו רק ארבעה מרווחים קלים אפשריים, כולל:

• שנייה מינורית
• שלישית מינורית
• מינורי השישי
• מינורי שביעי

לפני שנמשיך הלאה, בואו נסכם את מה שכבר למדנו:

• אם אתה מסתכל על התו העליון בסולם מרכזי החל מתו הטוניק או השורש, זה יכול להיות רק מרווח מרכזי או מושלם.
• אם התו העליון בסולם הראשי הוא רביעי, חמישי או שמיני, יהיה לך מרו וח מושלם.
• אם התו העליון בסולם הראשי הוא שני, שלישי, שישי או שביעי, אז יהיה לך מרווח גדול.
• אם אתה לוקח את התו העליון של מרווח מרכזי ומוריד אותו בחצי טון או חצי צעד, יהיה לך מרווח קטן.

מרווחים מוגברים

כאשר אתה מאריך מרווח גדול או מושלם בחצי צעד או חצי טון, אם כי שומר על אותו שם אותיות, אתה מקבל מרווח מוגבר.

כך, למשל, אם היינו לוקחים מרווח חמישי מושלם, כגון C ל- G, ואנחנו מרחיבים את ה- G ל- G #, היינו הופכים אותו למרווח חמישי מוגבר. אותו דבר היה קורה אם ניקח מרווח שני מרכזי C עד D ונארחיב את ה- D ל- D #. מרווח זה יהיה מרווח שני מוגבר.

התבונן בתמונה למטה כדי לקבל מושג טוב יותר כיצד נראים מרווחים מוגברים, ואל תהסס לקחת שנייה ולנגן אותם במקלדת אם יש לך כזה בסביבה כדי להתרגל לאיך שהם נשמעים.

אז מה קורה אם נשים דירה על התו הגבוה יותר במרווח במקום חד?

במקרה כזה, אנו מקבלים מה שנקרא מרווח מופחת.

מרווחים מופחתים

אם נניח דירה על אחד מהמרווחים המושלמים (רבעים, חמישיות או שמיניות), הם הופכים למרווחים מופחתים, ולא למרווחים קלים.

לדוגמה, נניח שיש לנו את התווים C עד F, שהם רביעי מושלם.

אם היינו שמים דירה על הפתק F כדי להפוך אותו ל- Fb, היינו מקבלים רביעי מופחת.

אם נשים שטוח על מרווח קטן כדי להוריד את התו העליון בחצי טון, נקבל גם מרווח מופחת. לדוגמה, אם יש לנו את התווים E עד D, שהם שביעית מינורית, ונניח דירה על ה- D כדי להוריד אותו בחצי טון אחד, היינו מקבלים שביעי מופחת.

אם היינו רוצים להפוך מרווח גדול למרווח מופחת, היינו צריכים לשטח את התו העליון בצעד שלם במקום זאת.

עריכת מרווחי מוסיקה סטנדרטיים

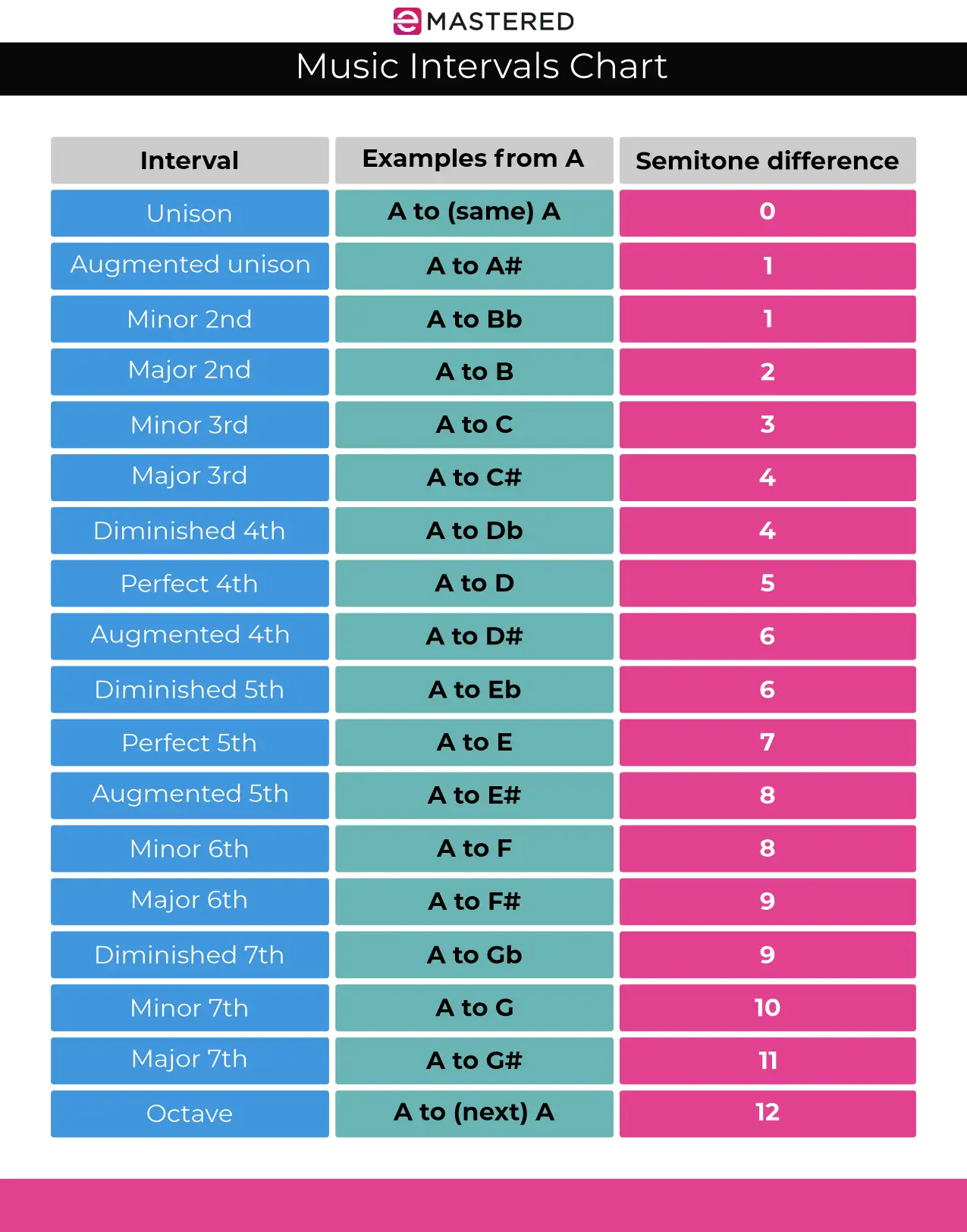
בשלב זה, אתה צריך הבנה די הגונה של איך מרווחים עובדים במוזיקה. להלן תרשים קטן שתוכל לקחת איתך כדי לזכור את המרווחים השונים מאוחד לאוקטבה:

מרווחים מורכבים

עד כה דנו מהם מרוו חים פשוטים.

מרווח פשוט הוא כזה שנמצא בתוך אוקטבה אחת. עם זאת, כאשר אנו יוצאים מחוץ לגבולות אוקטבה, אנו נכנסים למה שנקרא מרווחים מורכבים.

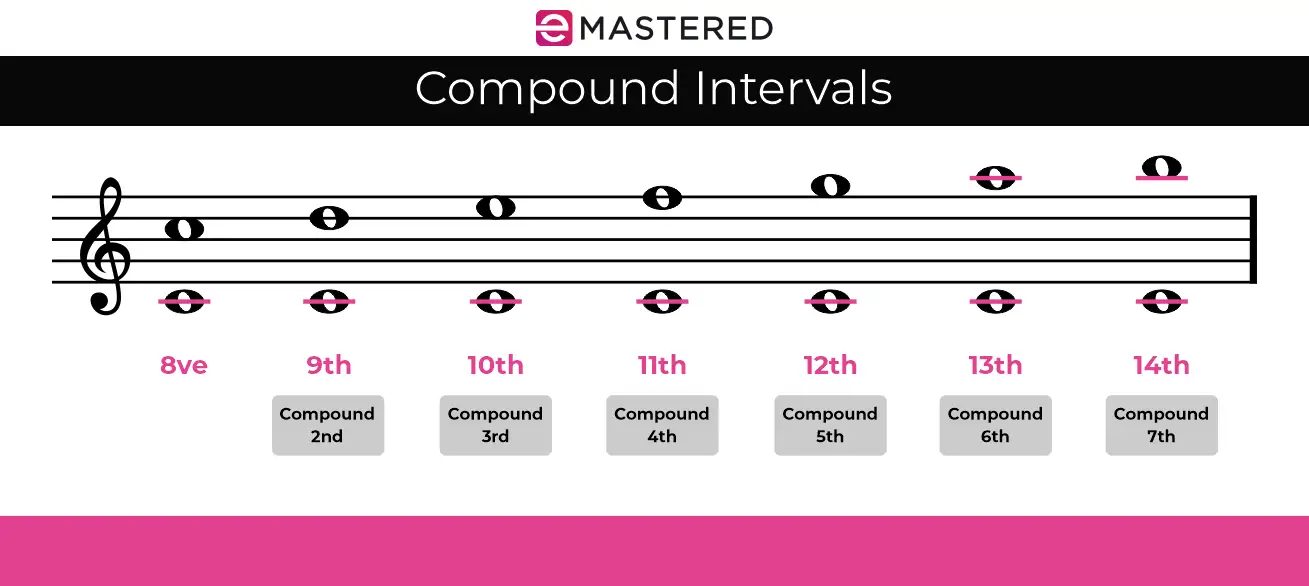
ישנן כמה דרכים שונות לדון במרווחים מורכבים.

השיטה הראשונה היא באמצעות המילה "תרכובת" מול שם המרווח.

לדוגמה, נניח שהיה לנו מרווח C עד E, שאנו יודעים כעת שהוא שליש מרכזי.

אם היינו לוקחים את התו העליון E ומניחים אותו באוקטבה אחת גבוה יותר, הוא היה הופך לשליש גדול מורכב.

עם זאת, ניתן גם למנות מרווחים מורכבים באמצעות שמות מספרים מעל שמונה.

באותה דוגמה לעיל, ה- C עד E עם E שהוא גבוה באוקטבה יהיה עשי רית גדולה במקום של יש גדול מורכב.

מרווחים הרמוניים ומלודיים

מעבר לשימוש במספרים ובאיכות להגדרת מרווחים, תיאורטיקני המוזיקה מסווגים לעתים קרובות מרווחים בשתי קבוצות שונות, כולל:

• מרווחים הרמוניים
• מרווחים מלודיים

בעוד שהם משתמשים באותם מונחים, מרווחים הרמוניים ומרווחים מלודיים שונים מסולמות מינוריות הרמוניות ומלודיות.

מרווחים הרמוניים

מרווח הרמוני הוא מרווח שבו שני התווים מנוגנים יחד או ב"הרמוניה".

אם תסתכל על התמונה למטה, תראה C ו- E מנוגנים בו זמנית ליצירת שליש מז'ור הרמוני.

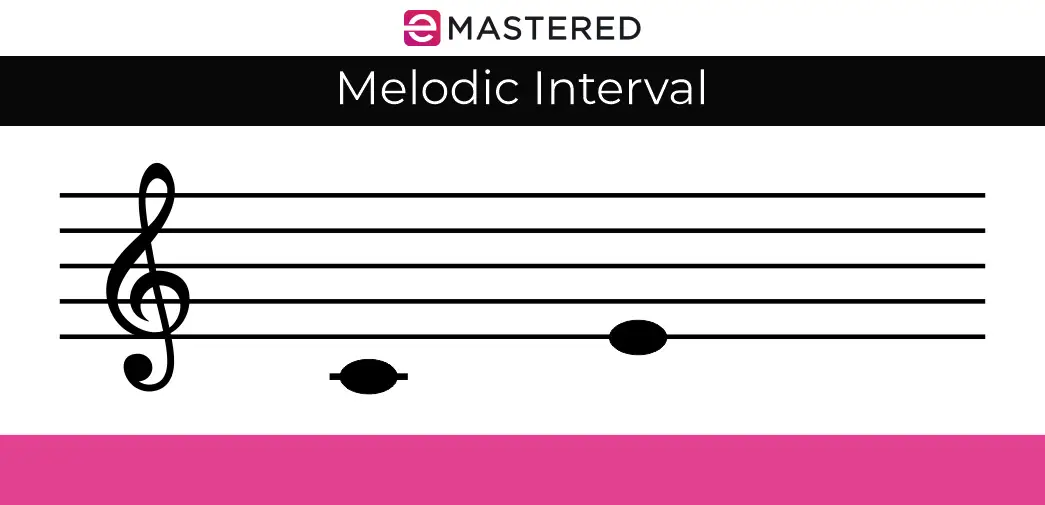
מרווחים מלודיים

מצד שני, יש לנו מרווחים מלודיים שבהם מנגנים תו אחד אחרי השני. מכיוון שאומרים כי התווים הללו הם חלק מנגינה, הם נקראים מרווחים מלודיים.

אם תסתכל על התמונה למטה, תראה C ו- E מנו גנים בצורה המלודית ליצירת שליש גדול מלודי.

מרווחים במוזיקה

כשמדובר בזיהוי מרווחים במוזיקה, הדבר הראשון שעליך לעשות הוא להבין את המושגים התיאורטיים שלהם, שכבר כיסינו לעיל. ברגע שאתה מרגיש בנוח עם האופן שבו המרווחים עובדים באופן כללי, אתה יכול להתחיל ללמוד כיצד לזהות אותם לפי האוזן.

בואו נצא למסע קטן במרווחים השונים במוזיקה ונדון בכמה שירים פופולריים שיעזרו לכם לזהות אותם בקלות.

מינורי שני

השנייה הקטנה היא המרווח הקטן ביותר בתורת המוזיקה המערבית.

עם חצי צעד או חצי טון בין שני התווים, אתה מקבל אפקט דיסוננטי ומרער רעות כאשר שני התווים מנוגנים זה ליד זה או בו זמנית.

אחת הדוגמאות הטובות ביותר לשנייה מינורית היא שיר הנושא מהסרט "לסתות".

תווי ההיכרות בשיר נעים למעלה ולמטה בצורה שנייה מינורית כדי לעורר אימה בלבם ובמוחם של המאזינים. אפילו עשרות שנים לאחר מכן, שיר הנושא לסרט זה עדיין ניתן לזיהוי מיידי!

מייג'ור שני

זה נראה די טיפשי שנוכל פשוט לקחת את התו העליון בשנייה הקטנה המאיימת ולהעלות אותו בחצי צעד כדי לקבל את תווי ההתחלה של אחד השירים המאושרים ביותר על פני כדור הארץ!

בשורה הראשונה של "יום הולדת שמח", אתה יכול לשמוע שנייה גדולה עולה ויורדת.

השנייה הגדולה העולה היא Hap py - לידה, ואילו השנייה הגדולה היו רדת היא יום הלידה.

שלישית מינורית

את השליש הקטין ניתן למצוא בשיר האנגלי המסורתי, "Greensleeve". ישנם שלישים קלים רבים לאורך השיר הזה, אם כי אתה יכול לשמוע את המרווח השלישי העולה הראשון בתחילת השיר.

עבור שליש מינור יורד, אחת הדוגמאות הטובות ביותר לשיר מגיעה מ- "היי ג'וד", ללא ספק אחד משירי הביטלס הפופולריים ביותר בכל הזמנים.

אתה יכול לשמוע את השליש המיני היורד הזה בשורה הראשונה של השיר שעובר מ- "היי" ל"ג'וד".

מייג'ור שלישי

כשחוזרים למרווחים המאושרים יותר, אחת הדוגמאות הטובות ביותר לשיר של השליש הגדול מגיעה מהרוחני האמריקאי הישן, "כאשר הקדושים הולכים לצעוד פנימה".

ניתן לשמוע את השליש הגדול העולה בשורה הראשונה של השיר, מ- "Oh" ל- "When".

מצד שני, הדוגמה הטובה ביותר לשליש גדול יורד מגיעה מהרוחני האפרו-אמריקאי, "Swing Low, Sweet Chariot".

אתה יכול לשמוע את השליש המיני היורד בשורה הראשונה של השיר כשהוא עובר מ- "Swing" ל- "Low".

הרביעי המושלם

לצד החמישית המושלמת, הרביעי המושלם הוא אחד המרווחים היציבים ביותר בתורת המוזיקה המערבית.

אחת הדוגמאות הטובות ביותר לרביעי המושלם במוזיקה פופולרית מגיעה מהמזמור הנוצרי מהמאה ה -18, "חסד מדהים".

אתה יכול לשמוע את הרביעי המושלם העולה הזה בהברה הראשונה של השיר במילה "A- maz -ing".

דוגמה מצוינת למרווח רביעי מושלם יורד היא משיר חג המולד האהוב, "בוא, כולכם נאמנים".

ניתן לשמוע את הרביעי היורד הזה בשורה הראשונה, מהמילים "או בוא" ל"הכל".

טריטון

הטריטון הוא אחד המרווחים הלא שגרתיים והמטרידים ביותר במוזיקה המערבית. במשך שנים רבות אנשים התייחסו אליו כאל "מרווח השטן". טריטון יושב ממש בין המרווחים הרביעיים המושלמים לחמישי המושלם. ניתן להתייחס אליו כאל רביעי מוגבר או חמישי מופחת.

אחת הדוגמאות הטובות ביותר לטריטון במוזיקה המערבית היא שיר הנושא של משפחת סימפסון. אתה יכול לשמוע את הטריטון בשורה הראשונה, "הבנים של סי מפ".

באשר לדוגמא יורדת לטריטון, האזינו לשיר "Even Flow" מאת פרל ג'אם.

הקו הקולני בפסוק הראשי מתחיל במרווח טריטון בולט.

החמישי המושלם

החמישית המושלמת היא אחד המרווחים היציבים ביותר בתורת המוזיקה המערבית. תמצא שהוא משמש בכבדות בשלשות בסיסיות, והוא מהווה את רוב התקדמות האקורדים במוזיקה פופולרית.

כאשר הוא מנוגן כמרווח הרמוני, הוא יוצר צליל חזק מאוד. מצד שני, כאשר משתמשים במנגינה, אתה יכול ליצור צליל מרומם או מנצח.

אחת הדוגמאות הטובות ביותר לחמישית המושלמת ניתן למצוא בשיר הנושא של מלחמת הכוכבים.

לדוגמא מרווח חמישי מושלם יורד, תוכלו להאשיב לתווים הראשונים בשיר הנושא של The Flinstones. ניתן לשמוע את החמישית המושלמת היורדת על "אבני הפלין" הראשונות.

מינורי השישי

ברגע שאנחנו מגיעים מעל החמישית המושלמת, המרווחים מתחילים להרגיש הרבה יותר "מלודיים". המרחק בין שני התווים במרווחים שישיים קלים ומעלה גדול בהרבה, וכאן דוגמאות השירים מתחילות להיות מועילות בהרבה.

אחת הדוגמאות הטובות ביותר לשישית הקטנה במוזיקה פופולרית מודרנית מגיעה מהלהקה FUN ושיר הלהיט שלהם, "We Are Young".

אתה יכול לשמוע את זה במקהלה בשורה "הגדר את העולם על אש".

דוגמה נהדרת נוספת לשישית מינורית במוזיקה הנעה בין שישית מינורית עולה ויורדת מגיעה ממנגינת הראגטיים הקלאסית של סקוט ג'ופלין, "הבדרן".

אתה יכול לשמוע את הקטין השישי נע למעלה ולמטה אחרי שני פתקי האיסוף הראשונים.

מייג'ור השישי

המרווח השישי העיקרי הוא עוד קפיצה די גדולה שבה דוגמה טובה לשיר יכולה להועיל.

אחת הדוגמאות הטובות ביותר לשישית גדולה במוזיקה מגיעה משיר העם הסקוטי המסורתי, "בוני שלי שוכבת מעל האוקיינוס".

אתה יכול לשמוע את השישי הגדול העולה בהברות הראשונות של השורה הראשית, "My Bon -nie".

באשר לדוגמא טובה לשישית יורד, אתה יכול להשתמש ב"איש במראה" מאת מייקל ג'קסון.

אתה תמצא שישית יורד במקהלה על שתי ההברות הראשונות, "אני מתחיל עם האיש במראה."

מינורי שביעי

אחת הדוגמאות הטובות ביותר לשביעית הקטנה במוזיקה מגיעה מ - West Side Story.

אתה יכול לשמוע את המז'ור השביעי העולה הזה בשיר "אי שם" בש ורה "יש לנו מקום".

באשר לשביעית מינורית יורדת, אחת הדוגמאות הפופולריות ביותר מגיעה מ"איש אבטיח" מאת הרבי הנקוק. שני התווים הראשונים בשיר מהווים מרווח שביעי קטן.

מייג'ור שביעי

המרווח השביעי העיקרי הוא מרווח מוזר שלא נמצא לעתים קרובות במוזיקה פופולרית, מכיוון שהוא כל כך קרוב לאוקטבה. כמובן שלעתים קרובות תשמעו את המרווח באקורדים, במיוחד לקצת צבע נוסף.

אחת הדוגמאות הפופולריות ביותר לשביעי הגדול כמרווח מלודי היא מהקלאסיקה A-Ha, "Take On Me".

אתה יכול לשמוע את המרווח השביעי העיקרי בשורה הראשונה של המקהלה, "Take On".

באשר לשביעי מז'ור יורד, אחת הדוגמאות הטובות ביותר מגיעה מהמנגינה בשיר של קול פורטר, "אני אוהב אותך".

התווים הראשונים של המנגינה מתחילים בטיפה שביעית גדולה נועזת.

אוקטבה

האוקטבה היא קפיצת המרווחים הפשוטה הגדולה ביותר בתורת המוזיקה. אחת הדוגמאות הטובות ביותר לקפיצת אוקטבה זו מגיעה מהשיר הפופולרי "Somewhere Over the Rainbow".

למקהלה יש קפיצת אוקטבה בין שתי ההברות של "Some- where".

אחת התזכורות האהובות עלינו לאוקטבות יורדות מגיעה משיר הנושא לסיטקום הפופולרי של שנות ה -90, ?$#@$ האוזר, M.D. אתה יכול לשמוע אותו בשורת הסינתזה ממש בתחילת השיר.

מחשבות אחרונות

מרווחים הם חלק מהכלים החשובים ביותר לתורת המוזיקה בסביבה. בלי הכלים הבסיסיים האלה לתורת המוזיקה, אתה לא יכול להגיע רחוק מאוד. ממנגינות לאקורדים ועד התקדמות ומעבר לכך, אתה יכול לחשוב על מרווחים כאבני בניין.

כעת, לאחר שעברת את המאמר הזה, אמור להיות לך מושג טוב כיצד לזהות מרווחים במוזיקה שאתה אוהב ולהשתמש במרווחים בזמן שאתה כותב מוזיקה משלך.